Carnot Cycle

ChemiCalcHub

The Carnot cycle is a theoretical thermodynamic cycle that serves as an idealized model for the operation of heat engines. It was developed by the French engineer Sadi Carnot in 1824 and is often used as a benchmark for the maximum efficiency that any heat engine can achieve operating between two temperature reservoirs.

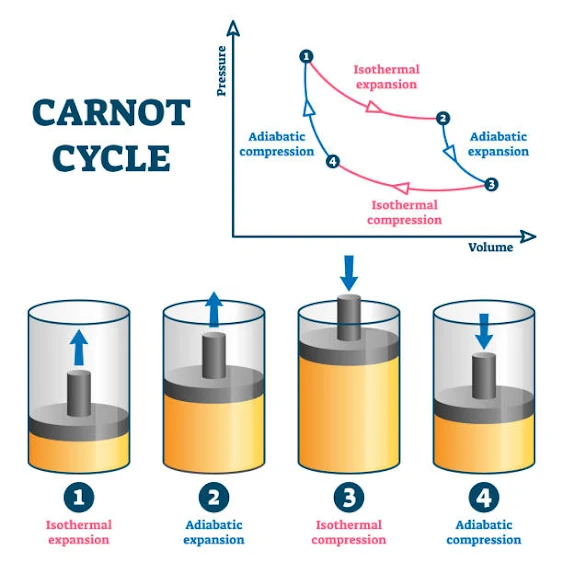
The Carnot cycle consists of four reversible processes:

1. Isothermal Expansion (Isothermal Heating):In this stage, the working substance (often a gas) is in contact with a high-temperature reservoir (a heat source) and undergoes an isothermal process. During this process, heat is added to the gas, and it expands while maintaining a constant temperature. The gas does work on a piston, and its internal energy increases.

2. Adiabatic Expansion: After the isothermal expansion, the gas undergoes an adiabatic (no heat transfer) expansion. During this process, the gas continues to do work on the piston, and its temperature decreases. This is an inherently reversible process.

3. Isothermal Compression (Isothermal Cooling): In this stage, the working substance is placed in contact with a low-temperature reservoir (a heat sink), and it undergoes another isothermal process, but this time it is compressed. Heat is extracted from the gas, and it contracts while maintaining a constant temperature. The gas does work on the piston, and its internal energy decreases.

4. Adiabatic Compression: Finally, the gas undergoes an adiabatic compression, where it is further compressed without heat transfer, resulting in an increase in temperature.

The Carnot cycle is often represented on a pressure-volume (PV) diagram, where it forms a closed loop. The efficiency of a Carnot engine, denoted by "η," is given by the formula:

\[η = 1 - \frac{Tc}{Th}\]

Where:

- η is the efficiency of the engine (expressed as a decimal or percentage).

- Tc is the absolute temperature of the cold reservoir (in Kelvin).

- Th is the absolute temperature of the hot reservoir (in Kelvin).

The Carnot cycle represents the maximum theoretical efficiency that any heat engine operating between two temperature reservoirs can achieve. It serves as a useful reference point for comparing the actual performance of real-world heat engines, such as steam engines and internal combustion engines. These real engines cannot achieve the Carnot efficiency due to various irreversibility and losses in the actual processes. However, the Carnot cycle sets the upper limit that no heat engine can surpass when operating between the same temperature reservoirs.

Calculating the efficiency of a Carnot cycle involves using the formula:

\[η = 1 - \frac{Tc}{Th}\]

Where:

- η is the efficiency of the Carnot cycle (expressed as a decimal or percentage).

- Tc is the absolute temperature of the cold reservoir (in Kelvin).

- Th is the absolute temperature of the hot reservoir (in Kelvin).

Here's how you can perform a Carnot cycle calculation:

1. Determine the Temperatures:Identify the temperatures of the hot reservoir (Th) and the cold reservoir (Tc) in Kelvin. Ensure that the temperatures are measured on an absolute temperature scale (Kelvin or Rankine) to maintain consistency with the formula.

2. Calculate Efficiency: Plug the values of Th and Tc into the formula and perform the calculation. The result will be the efficiency of the Carnot cycle.

3. Convert to Percentage (Optional): If you want to express the efficiency as a percentage, multiply the calculated efficiency (as a decimal) by 100.

Let's do an example calculation:

Suppose you have a Carnot engine operating between a hot reservoir at 500 Kelvin (Th = 500 K) and a cold reservoir at 300 Kelvin (Tc = 300 K).

\[η = 1 - \frac{300}{500} = 1 - 0.6 = 0.4\]

So, the efficiency of the Carnot cycle in this case is 0.4, or 40% if expressed as a percentage.

This means that for this Carnot engine, 40% of the heat input is converted into useful work, and the remaining 60% is rejected to the cold reservoir. The Carnot cycle represents the theoretical upper limit of efficiency for any engine operating between these two temperature reservoirs. Real engines typically have lower efficiencies due to various irreversibilities and losses in their operation.

Carnot Cycle Calculator

Temperature of Hot Reservoir (K):

Temperature of Cold Reservoir (K):

Results